Random Walks to solve Diophantine Equations

Random walks (check my older post here) and Diophantine equations are two simple mathematical beasts. After a college seminar, I tried putting them together to make something neat, and came up with this: just pick a Diophantine equation, simulate a random walk, and try to see if the random walk went over any solutions! In this report I briefly go over how I came up with this, and show the code I wrote/some results. The Matlab code is all in here (I also have some Python code about random walks in general here, check my post!).

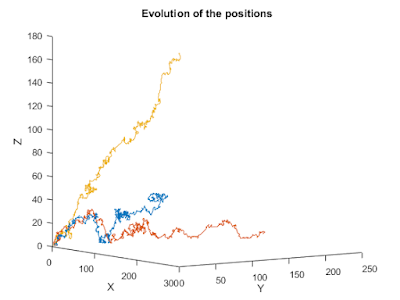
In the image above, the blue line represents a path taken by the random walk and in orange/red the nodes tell us how far we are from a solution (the smaller the node, the closer we are). Note that this notion of proximity isn't given by actually computing the distance to a known solution, but just by looking at how similar the two sides of the equation are. The image below shows the evolution of three independent random walks trying to find an example solution of $\frac{4}n = \frac1x + \frac1y + \frac1z$ with $n = 25$ (that expression is the expression of the Erdos-Straus conjecture).

[Pt] Passeios aleatórios (vejam o meu post anterior)  e equações Diofantinas são dois assuntos matemáticos de grande interesse. Depois de um seminário na faculdade, tentei juntar os dois para fazer algo de interessante e foi isto que inventei: tentar usar um caminho aleatório para encontrar soluções de uma equação Diofantina! Neste relatório, tento explanar como decidi fazer isso, e como o concretizei com uma implementação em Matlab (disponível aqui) que, em particular, produziu as duas imagens deste post.

Na primeira imagem, a linha a azul representa um caminho aleatório, e os nós a vermelho/laranja representam o quão próximo esses pontos estão de soluções. Na segunda imagem vemos a evolução de três caminhos aleatórios que estão a procurar uma solução de $\frac4n = \frac1x + \frac1y + \frac1z$ com $n = 25$, que é a expressão da conjetura de Erdos-Straus.

Let me know what you think!

-RGS